Excel中标准偏差计算的简易公式

标准偏差计算公式在Excel中的应用

在数据分析领域，标准偏差（Standard Deviation，简称SD）是衡量数据分布离散程度的一个重要指标。Excel作为一款功能强大的电子表格软件，内置了多种计算函数，可以方便地对数据进行标准偏差的计算。本文将详细介绍如何在Excel中使用标准偏差计算公式，并通过实例演示具体操作步骤。

一、标准偏差的概念

标准偏差是描述数据集中各数值与平均值之间离散程度的一个量度。具体来说，它反映了每个数值与平均值的偏差平方的平均数的平方根。标准偏差越小，说明数据集中的数值越接近平均值，数据的离散程度越小；反之，标准偏差越大，说明数据集中的数值与平均值的差异越大，数据的离散程度越大。

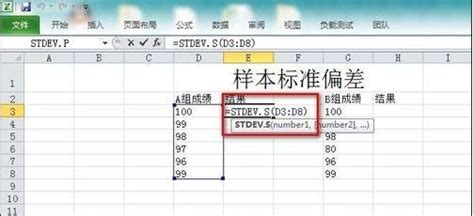
二、Excel中的标准偏差函数

在Excel中，标准偏差的计算主要依靠内置的函数来实现。主要有以下几个相关函数：

1. STDEV.P：计算基于整个数据集的总体标准偏差（Population Standard Deviation）。如果数据代表整个总体，应使用此函数。

2. STDEV.S：计算基于样本数据集的样本标准偏差（Sample Standard Deviation）。如果数据是从一个更大的总体中随机抽取的样本，应使用此函数。

3. STDEVA：计算包含文本和逻辑值的样本标准偏差（忽略N/A错误值）。这个函数类似于STDEV.S，但能够处理文本和逻辑值，将其视为0。

三、标准偏差的计算公式

标准偏差的计算公式分为总体标准偏差和样本标准偏差两种：

1. 总体标准偏差公式：

\[

\sigma = \sqrt{\frac{\sum_{i=1}^{N}(x_i - \mu)^2}{N}}

\]

其中，$\sigma$ 表示总体标准偏差，$x_i$ 表示数据集中的每个数值，$\mu$ 表示数据的平均值，$N$ 表示数据的总数。

2. 样本标准偏差公式：

\[

s = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}}

\]

其中，$s$ 表示样本标准偏差，$x_i$ 表示样本中的每个数值，$\bar{x}$ 表示样本的平均值，$n$ 表示样本的数量。注意这里分母是 $n-1$，即自由度（degrees of freedom）的调整，也称为贝塞尔修正（Bessel's correction）。

四、在Excel中计算标准偏差

1. 使用STDEV.P计算总体标准偏差

假设有一组数据存储在Excel的A1:A10单元格中，步骤如下：

1. 选中一个空白单元格，用于显示计算结果。

2. 输入公式：`=STDEV.P(A1:A10)`。

3. 按下回车键，Excel将计算并显示这组数据的总体标准偏差。

2. 使用STDEV.S计算样本标准偏差

同样以A1:A10单元格中的数据为例，步骤如下：

1. 选中一个空白单元格，用于显示计算结果。

2. 输入公式：`=STDEV.S(A1:A10)`。

3. 按下回车键，Excel将计算并显示这组数据的样本标准偏差。

3. 使用STDEVA计算包含文本和逻辑值的样本标准偏差

假设A1:A10单元格中可能包含一些文本或逻辑值，步骤如下：

1. 选中一个空白单元格，用于显示计算结果。

2. 输入公式：`=STDEVA(A1:A10)`。

3. 按下回车键，Excel将计算并显示这组数据的样本标准偏差，忽略其中的文本和逻辑值（将其视为0）。

五、实例演示

示例数据

假设有以下数据集，存储在Excel的A列中：

| A列 | 数据 |

|||

| A1 | 5 |

| A2 | 10 |

| A3 | 15 |

| A4 | 20 |

| A5 | 25 |

| A6 | 30 |

| A7 | 35 |

| A8 | 40 |

| A9 | 45 |

| A10 | 50 |

计算总体标准偏差

1. 在B1单元格中输入公式：`=STDEV.P(A1:A10)`。

2. 按下回车键，得到总体标准偏差为15.811