角度与弧度转换公式详解

在数学中，角度与弧度是描述平面上角的大小的两种不同单位。尽管它们在日常应用和教学中都有广泛的使用，但理解它们之间的转换至关重要。本文将从角度与弧度的基本概念、转换公式的推导、应用实例及在实际问题中的意义等多个维度探讨这一话题。

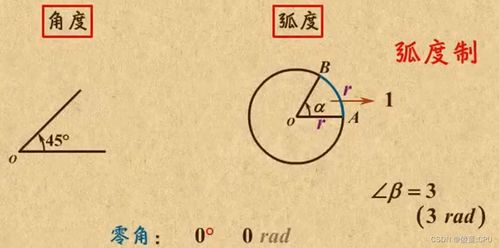
一、基本概念

角度

角度是我们日常生活中最为熟悉的角的大小度量方式。通常，一个完整的圆被分成360度（°），这是角度制的基本单位。在角度制中，一个直角等于90度，一个平角等于180度，一个周角则是360度。角度制的度量直观易懂，特别适合用于几何图形的直观分析和度量。

弧度

弧度则是基于圆周的另一种度量方式。在弧度制中，一个完整的圆周长与半径的比值定义为2π（pi），因此一个完整的圆的角度等于2π弧度（rad）。弧度的度量更加符合数学中的运算规律，尤其是在微积分和三角函数等领域，弧度制能够大大简化计算过程。

二、转换公式的推导

角度与弧度之间的转换基于圆的基本性质。具体转换公式如下：

1. 角度转弧度

\[

\text{弧度} = \text{角度} \times \frac{\pi}{180}

\]

这个公式将角度乘以π/180，转换成弧度。例如，90度转换为弧度就是：

\[

90 \times \frac{\pi}{180} = \frac{\pi}{2} \text{弧度}

\]

2. 弧度转角度

\[

\text{角度} = \text{弧度} \times \frac{180}{\pi}

\]

这个公式将弧度乘以180/π，转换成角度。例如，π/4弧度转换为角度就是：

\[

\frac{\pi}{4} \times \frac{180}{\pi} = 45 \text{度}

\]

这两个公式的推导基于圆的周长和半径之间的关系。一个圆的周长为2πr，其中r为半径。若一个圆被均匀分成360份，每一份的角度为1度，对应的弧长则为\( \frac{2\pi r}{360} = \frac{\pi r}{180} \)。因此，1弧度对应的弧长就是半径r，即\( \text{弧长} = r \)。于是，1弧度对应的角度就是\( \frac{\pi r}{180} \)除以r，简化后得\( \frac{\pi}{180} \)度，从而得出角度转弧度的公式。同理，弧度转角度的公式也可通过类似的推导得到。

三、应用实例

角度与弧度之间的转换在实际应用中具有广泛的意义，尤其在物理学、工程学、计算机科学和数学等领域。

物理学中的应用

在物理学中，特别是涉及圆周运动和波动现象的研究中，弧度制具有更为直观和方便的表示方式。例如，在描述简谐振动时，通常使用弧度制来表示振动的相位和频率。

工程学中的应用

在机械工程和电气工程领域，角度与弧度的转换也是必不可少的。例如，在控制系统中，电机转子的位置和速度通常通过弧度制来描述，以便更准确地计算和控制。

计算机科学中的应用

在计算机图形学和游戏开发中，角度与弧度的转换同样重要。例如，在三维渲染和动画中，旋转和位移的计算通常基于弧度制，以便实现平滑和连贯的视觉效果。

数学中的应用

在数学中，尤其是微积分和三角函数的研究中，弧度制具有显著的优势。例如，导数的定义和计算，以及三角函数的求导和积分，在弧度制下都更为简洁和直观。

四、实际问题的意义

角度与弧度之间的转换不仅是一个纯粹的数学问题，它还具有深远的实际意义。以下是一些具体的应用场景：

1. 精确计算

在工程设计和科学研究中，精确的计算是至关重要的。角度与弧度的转换能够确保计算结果的准确性和一致性，特别是在涉及圆周运动和波动现象的研究中。

2. 简化运算

在数学运算中，特别是在涉及三角函数和微积分的计算中，弧度制能够大大简化运算过程。使用弧度制可以避免许多复杂的转换和计算步骤，从而提高计算效率。

3. 统一度量标准

角度与弧度是两种不同的度量标准，但它们之间是可以相互转换的。这种转换能力使得在不同的学科和领域中，可以根据实际需要选择合适的度量标准，从而实现度量标准的统一和协调。

4. 促进跨学科研究

随着科学技术的发展，跨学科研究已成为一种趋势